今天在arXiv上读到了一篇非常有趣的论文,由MIT的物理学家Max Tegmark撰写,名为《 Consciousnessas a State of Matter》(作为物质状态的意识)。他认为,自我意识可以认为是某种物质形态,如文中的表一所示,意识必须同时包含有长期存在的状态,集成化的信息,容易写入性,以及复杂的动力学。气体,液体,固体,乃至计算机都只能满足一部分判据。
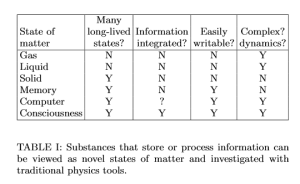 为了解释意识可以被看成是物质的一种形态,他提出了六条原理,见表二
为了解释意识可以被看成是物质的一种形态,他提出了六条原理,见表二

利用这些原理,他主要研究了”量子因子分解问题“,或者说作为一个有意识的的观察者,比如说我们,为什么可以感受特定的希尔伯特空间分解所对应的经典空 间,而不是傅里叶空间。或者更一般的,为什么我们把周围的世界理解为动态的层级,其中包含许多强烈集成且相对独立的物体。他认为,这个原理与所谓的从头开 始物理问题(physics-from-scratch)有关:我们如何才能从不过两个厄米矩阵中提取出三维空间和我们周围的半经典世界。能否仅从哈密顿 量H中提取出这些信息,而H完全可以仅从它的本征能谱来描述。
接下来,Max Tegmark详细的讨论了什么叫做Integration(整体性)。在他看来,我们的世界是分层次的客体。比如说,你正在喝一杯冰水,你会感受到在玻 璃杯中有冰块。玻璃和冰块是分立的客体,因为它们都各自是一个整体且相对独立,它们内部的联系远远比与外部的联系紧密。我们可以定义物体的稳定性为集成温 度(把整体分离为部分所需的能量密度)和独立性温度(在层级内把母辈物体分离开所需的能量密度)之比。比如说,冰块的独立温度大概是3毫开,集成温度大概 是300开,稳定性是 。在下一级的结构中,氧原子和氢原子的稳定性都是10。氧原子核的稳定性是
。在下一级的结构中,氧原子和氢原子的稳定性都是10。氧原子核的稳定性是 。稳定性越高,这个物体越容易被我们感知和定义。
。稳定性越高,这个物体越容易被我们感知和定义。
他发现,利用纠错码,经典物理允许信息基本上完全地被集成。任意一个包含至少半个比特的信息的子系统就可从剩下的比特中重建出来。存储在Hopeld neural networks (Hopeld神经网络)中的信息是天然的可纠错的。但是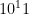 个 神经元只能支持大概37个比特的集成了的信息。这就带来了一个集成化的悖论:为什么在我们意识体验所包含的信息内容似乎远大于37个比特。更糟的是,他发 现把这个结果推广到量子信息领域,反而加重了集成性悖论:量子信息系统只能支持不多于四分之一集成化的比特。实际上,对于任意大的量子系统,无论我们如何 编码,它所包含的可集成的信息都不会超过四分之一个比特。这强烈的暗示我们,集成性原理至少需要一个附加的原理作为补充。
个 神经元只能支持大概37个比特的集成了的信息。这就带来了一个集成化的悖论:为什么在我们意识体验所包含的信息内容似乎远大于37个比特。更糟的是,他发 现把这个结果推广到量子信息领域,反而加重了集成性悖论:量子信息系统只能支持不多于四分之一集成化的比特。实际上,对于任意大的量子系统,无论我们如何 编码,它所包含的可集成的信息都不会超过四分之一个比特。这强烈的暗示我们,集成性原理至少需要一个附加的原理作为补充。
他接下来探讨了独立性原理,讨论了如何通过希尔伯特空间分解实现其对应的哈密顿量分立为互相独立的部分。他发现了量子芝诺效应悖论:如果我们把宇宙分为最 为相互独立的几个客体,那么所有的运动都会陷入中止。既然有意识的的观察者显然没有感受到任何的停滞,那么集成性和独立性原理必须还需要至少一个原理来作 为补充。
进一步的,他研究了动力学原理,因为有意识的系统不仅能存储信息,还要能处理它。他认为能量相干性(energy coherence)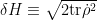 可以作为动力学的合适度量,它与时间无关,且在某些纯态情况下约化为能量的不确定性
可以作为动力学的合适度量,它与时间无关,且在某些纯态情况下约化为能量的不确定性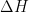 。把动力学最大化只会导致无聊的周期解,无法支撑复杂的信息处理。但是减小
。把动力学最大化只会导致无聊的周期解,无法支撑复杂的信息处理。但是减小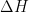 到合适的值时,将出现混沌和复杂的动力学,能遍历希尔伯特空间的所有维度。他 发现高度的自主性(独立性和动力学原理的结合)即使在一个高度开放的系统中也是可以实现的。
到合适的值时,将出现混沌和复杂的动力学,能遍历希尔伯特空间的所有维度。他 发现高度的自主性(独立性和动力学原理的结合)即使在一个高度开放的系统中也是可以实现的。
由上可知,Max Tegmark并未解决量子分解问题,但是这些结果可以帮助人们聚焦问题,并能强调具体的公开子问题和从观察得来的各种暗示和线索 。他还提出了一些公开的问题:
- 因子分解和鸡与蛋的问题:量子态和分解哪个先哪个后?
- 因子分解和集成化悖论
- 因子分解和时间的浮现